Artigo Técnico

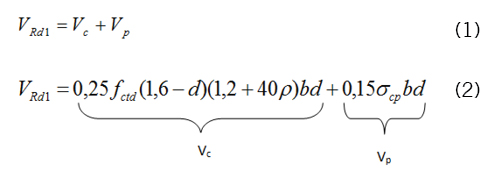
Apesar dos modelos de cálculo serem empíricos, a parcela Vp é proposta a partir de uma dedução analítica. Esta dedução toma por base uma seção retangular de uma viga e o princípio proposto por Hedman e Losberg (1978). Este princípio diz que a resistência à força cortante de um elemento em concreto protendido é a soma da resistência do elemento em concreto armado com a parcela da força cortante gerada pelo carregamento que provoca a descompressão na seção analisada. Em outras palavras, após o momento de descompressão ser alcançado, um elemento de concreto protendido pode ser considerado como um de concreto armado.

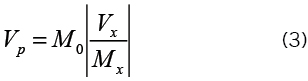
Vp pode então ser formulado como segue:
em que Mx é o momento fletor, Vx,o esforço cortante e M0, o momento de descompressão, todos na seção analisada. Pela equação acima, quando Mx for igual a Mo, ou seja, quando o momento de descompressão for atingido,Vp  é igual à Vx.
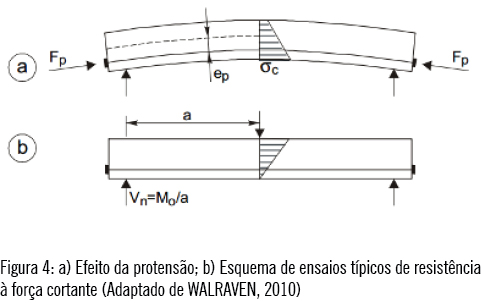
Considerando o ensaio típico para a verificação da resistência ao cisalhamento devido à força cortante, realizado nos laboratórios, a influência da protensão pode ser calculada como segue:

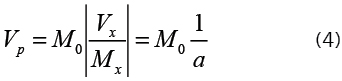
em que a é a distância da aplicação da carga até o centro do apoio mais próximo.

O momento de descompressão pode ser calculado isolando-se a variável Mo na equação a seguir. Esta equação descreve a situação em que as tensões nas fibras inferiores são nulas.

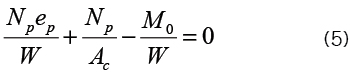
Isolando-se M_o,

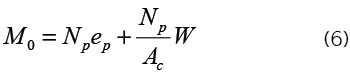
sendo W o módulo resistente da seção, Np a força normal de compressão devido à protensão na seção analisada, Ac a área da seção e ep a excentricidade de protensão.  
Para uma viga retangular com b de largura e h de altura, tem-se:

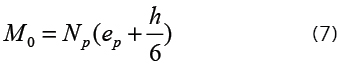
com h em evidência,

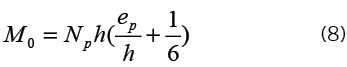
Considerando ep/h igual a 0,35, a equação acima passa a:

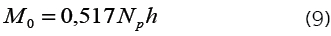
Assumindo a altura útilda seção, d, igual a 0,85h:

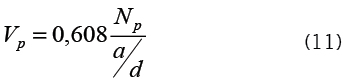
Com a distância de aplicação da carga até ao centro do apoio (ver Figura 4b) variando de 2,5d a 4d, como na maioria dos experimentos, e fazendo Np = σcpbd tem-se:

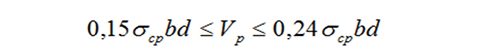
Desta forma, a parcela 0,15 σcpbd corresponde a   = 4, sendo o menor valor de Vp para o domínio de estabelecido.
Ao fixar a contribuição da protensão em 0,15 σcpbd, ao que tudo indica, buscou-se uma solução simples e prática para o mecanismo de flexo-cortante, uma vez que, desta forma, a influência da protensão na resistência à força cortante não varia com o tipo de carregamento, nem de seção a seção, sendo a única variação, aquela causada pela proporção de protensão introduzida na seção analisada (computada na variável σcp). 
Como descrito anteriormente, o domínio estabelecido de variação da ordem de 2,5 < < 4. Nota-se que quanto menor for esta relação, maior será a parcela Vp e, portanto, maior a resistência à força cortante. Isso significa, pelas premissas assumidas, que quanto mais difícil for descomprimir a seção pelo momento fletor atuante, maior a sua resistência à força cortante.
Para situações de lajes alveolares com alto nível de protensão e alto momento de inércia da seção transversal (lajes mais altas), descomprimir as seções próximas ao apoio se torna praticamente impossível. Desta forma, a potencial ruptura ocorre quando as tensões principais atingem a máxima tensão resistente de tração do concreto nas nervuras da laje alveolar, portanto, outro mecanismo faz-se presente, a tração diagonal.