ARTIGO TÉCNICO

O fator de maturidade pode ser calculado a partir de expressões matemáticas que relacionam a influência do tempo e da temperatura na hidratação do concreto (ASTM C 1074, 2011). De acordo com (fib Bulletin 1,1999), a função mais simples apresenta uma relação linear entre a taxa de hidratação e a temperatura, considerada como Equação de Nurse e Saul (Equação 1)

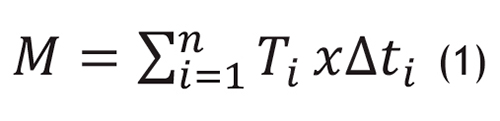
Onde:

Μ = fator temperatura-tempo (°C.dias);
∆ti = intervalo de tempo de cura na temperatura (dia);
Ti= temperatura durante um intervalo de tempo (°C)

Gonçalves (1986, apud SANTOS,2010), na equação acima a maturidade varia linearmente com a temperatura, porém sabe-se que devido à cinética das reações químicas, a velocidade do processo avança de forma exponencial. De forma a contemplar a não linearidade do ganho de maturidade, Arrehenius introduziu o conceito de energia aparente (Ea) nas equações  para quantificar a energias necessária para os reagentes tranformarem-se em produtos. Dessa forma, a velocidade de uma reação química é função de uma taxa constante KT, conforme mostra-se a seguir:

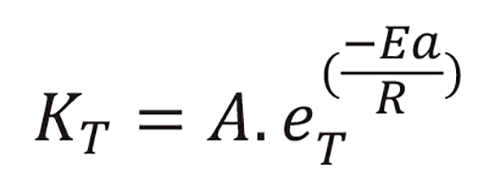
Onde:

KT= constante de velocidade à temperatura T;
Ea= energia aparente de ativação (J/mol);
R= constante universal dos gases (8,314 J/mol.K);
T= temperatura absoluta (K);
A= fator de frequência.

Devido aos avanços das pesquisas sobre maturidade, Saul reformulou a função incial elaborada por Nurse e Saul, adicionando uma variável em função da idade equivalente, como se mostra abaixo:

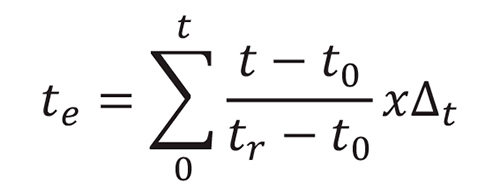
Onde:

tr= temperatura de referência (°C);
te= idade equivalente na temperatura de referência (h).

Rastrup (1954, apud SANTOS,2010) chegou a conclusão de que o concreto atinge o mesmo grau de maturidade  que atingiria caso tivesse sido mantido continuamente a uma temperatura  de referência até a idade equivalente. Com isso, Weaver e Sadgrove (1971, apud SANTOS,2010), desenvolveram uma nova equação usando a variável da idade equivalente:

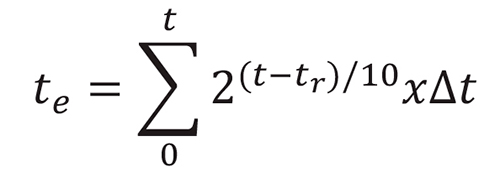
Onde:

tr= temperatura de referência (°C);
te= idade equivalente na temperatura de referência (h);
t= temperatura absoluta do concreto durante intervalo  ∆t (°C);
∆t= intevalo de tempo (h).

Freisleben-Hansen e Pedersen (FHP), que foram citados por Carino (1991, apud SANTOS 2010), elaboraram a equação que relaciona maturidade com a velocidade de hidratação do cimento  na temperatura desejada e na temperatura de referência (), como se mostra a seguir:

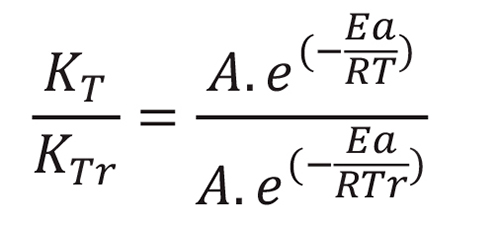
Onde:

KT= constante de velocidade à temperatura T;
KTr= constante de velocidade à temperatura Tr;
Ea= energia aparente de ativação (J/mol);
R = constante universal dos gases (8,314 J/mol.K);
T = temperatura absoluta (K);
Tr= temperatura de referência (K);
A = fator de frequência.

A função de maturidade proposta por Freisleben-Hansen e Pedersen, em idade equivalente, assume o seguinte formato:

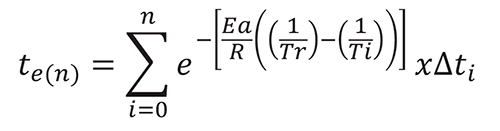
Em que:

Ea= energia aparente de ativação (J/mol);
R = constante universal dos gases (8,314 J/mol.K);
Ti= média da temperatura em um intervalo de tempo (h);
Tr= temperatura de referência (K);
∆ti= intervalo de tempo de cura na temperatura (dia);
te(n)= idade equivalente à temperatura de referência 

A função FHP é a que demonstra resultados mais satisfatórios do efeito real da temperatura na velocidade de reação de hidratação  do cimento, de acordo com Carino (1991, apud SANTOS 2010).