ARTIGO TÉCNICO

Figura 5: Esquema de ensaio (CEB FIP:1992 / EN 1168:2008)

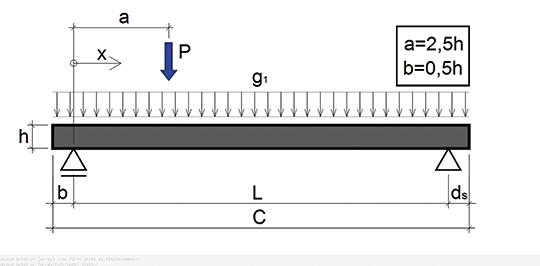
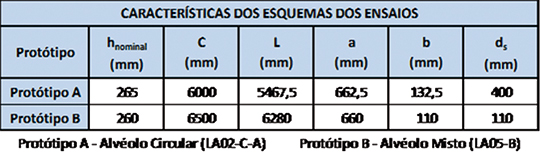
Tabela 3: Características dos esquemas dos ensaios

2.3. Geração da geometria das seções – Processo de cálculo
LINDSTROM (2007) definiu uma expressão para a determinação da geometria de alvéolos curvos, a qual foi reescrita na Equação 1.

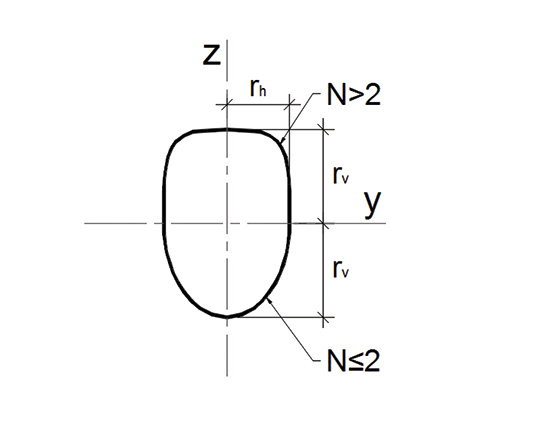
Os parâmetros rh e rv são medidas da semi-distância horizontal e vertical do centro geométrico do alvéolo até os extremos horizontais e verticais, respectivamente. Para melhor ilustrar a aplicação desta equação na definição geométrica dos alvéolos curvos apresenta-se a seguir a Figura 6 que denota inclusive o efeito que o fator de forma N tem sobre a curvatura, interferindo no grau de abatimento desta. Ou seja, quanto maior o parâmetro N, mais “achatada” é a curva.  Cada par de coordenadas (y,z) define um ponto do primeiro quadrante, onde y≥0 e z≥0. Quando N=2 a Equação 2 passa a ser a equação geral da elipse e se, além disso, rh=rv, obtém-se a equação da circunferência.

Figura 6: Características geométricas dos alvéolos curvos.

Para a determinação das formas dos alvéolos poligonais, foram definidos três segmentos de reta denominados “retas a, b e c” ilustradas conforme Figura 7.

Figura 7: Características geométricas dos alvéolos poligonais.

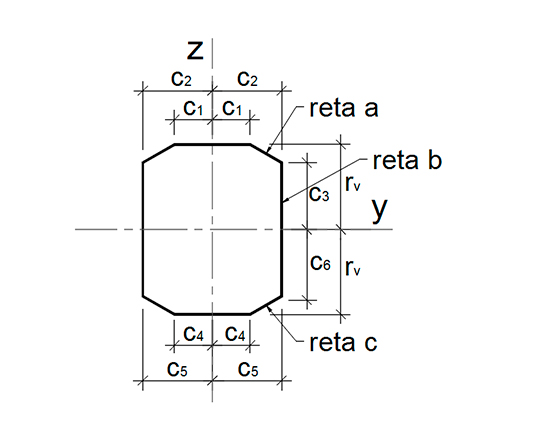
A “reta a” é definida pela Equação 2, bem como as Equações 3 e 4 definem as “retas b e c”, respectivamente.

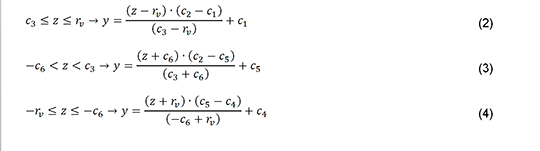
Para o cálculo das propriedades geométricas da seção transversal como: área (A), momento de inércia (Iy) e posição do centroide (zcg) foi adotada uma discretização por faixas tanto na obtenção das propriedades dos alvéolos (cujos parâmetros recebem o índice a) quanto para a seção transversal final da laje. Na Figura 8 a discretização dos alvéolos é ilustrada

Figura 8: Discretização dos alvéolos em faixas.

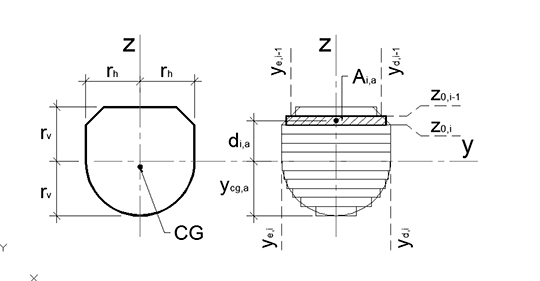
Com base na Figura 8 foram calculadas as propriedades de cada faixa do alvéolo (índice “i”) que somadas, posteriormente, compõem as propriedades do alvéolo integral, conforme passos algébricos definidos a seguir.

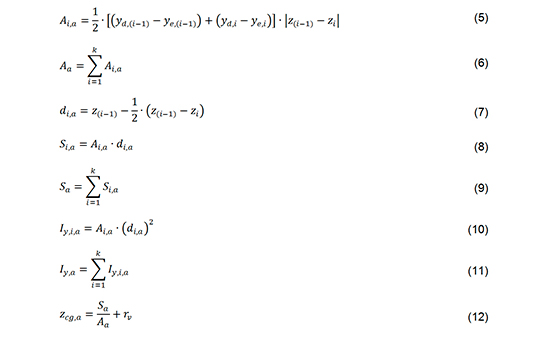
A discretização da seção transversal pode ser representada pela Figura 9. Nela é possível perceber que a origem dos eixos cartesianos foi deslocada para o centroide da seção transversal (no cruzamento entre os eixos), a fim de simplificar os cálculos posteriormente. Desta maneira, foi necessário fazer a mudança de coordenadas a partir daquelas definidas para o cálculo das propriedades geométricas dos alvéolos. Ou seja, os eixos de referência outrora chamados y e z, passaram a ser chamados y’ e z’.