ARTIGO TÉCNICO

Figura 9: Discretização da seção transversal em faixas.

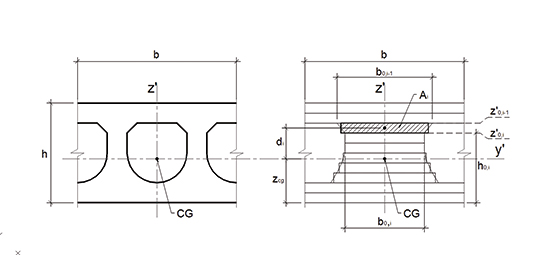
[Fonte: MACIEL (2017)]

Com base na Figura 9 e seguindo a mesma lógica do cálculo das propriedades dos alvéolos, são calculados todos os parâmetros que caracterizam a seção transversal analisada.

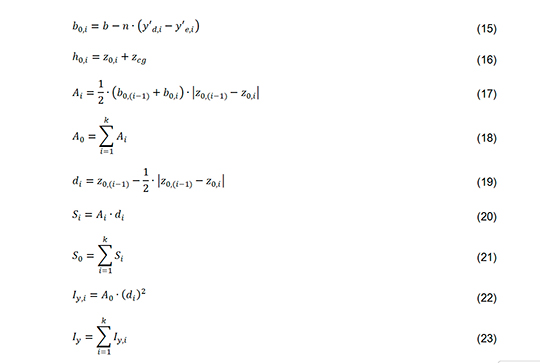
O índice 0 é adotado para definir a posição da seção analisada em relação a fibra inferior, onde é calculada a área acumulada (A0) e o momento estático acumulado (S0), como ilustrado na Figura 10. Este último por sua vez atinge seu valor máximo quando a coordenada z coincide com o centroide da seção e assim passa a receber a notação S. Estes parâmetros serão úteis para o cálculo da cortante resistente que será visto no próximo capítulo.

Figura 10: Parâmetros considerados da seção transversal.

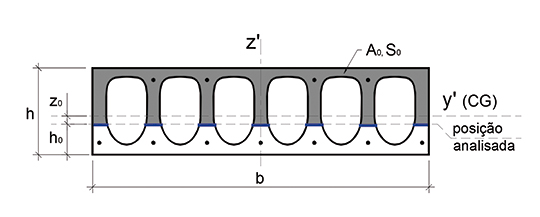
[Fonte: MACIEL (2017)]

Na Figura 11 apresentada a seguir ilustra-se algumas das possibilidades de formas de alvéolos geradas a partir da rotina de cálculo apresentada anteriormente.

Figura 11: Variações geométricas dos alvéolos

2.4. Modelo analítico normativo
Algumas normas internacionais apresentam duas equações distintas para o cálculo da força cortante resistente em lajes alveolares protendidas, considerando ou não a influência da fissuração. Porém, na normalização brasileira, a ABNT NBR 6118:2014 apresenta em seu texto apenas uma expressão que, por sua vez, foi fundamentada em estudos realizados para vigas protendidas retangulares sem armadura transversal e que consideram a ruptura por cisalhamento em zonas fissuradas. A norma de lajes alveolares, ABNT NBR 14861:2011, por sua vez, incorporou à mesma expressão apresentada na ABNT NBR 6118 um parâmetro ∂ de maneira inadequada, com o objetivo de considerar o efeito do comprimento de transferência que, a princípio, já havia sido contemplado no fator “0,15” da mesma equação. Esta duplicidade reduz significativamente o valor resistente calculado, conforme relatado por FRANÇA (2012). Assim, a título deste trabalho, será desprezado o fator ∂ para o cálculo dos valores apresentados posteriormente. Também será adotado para o valor da resistência a tração do concreto o valor característico inferior (f(ctk,inf)=0,7fctm)

Onde:
fctd: resistência a tração do concreto (minorada por yc); ∑b(w,1): somatório das nervuras internas e externas da seção transversal; As: área da armadura longitudinal tracionada; p1: taxa da armadura longitudinal; O(cp,1): tensão de compressão no concreto devido à força de protensão; Np: força de protensão final, depois de todas as perdas; Ac: área da seção transversal de concreto da laje; lx: distância da extremidade da laje até a seção em análise; lpt2: comprimento de transferência de protensão, fixado em 85Ø, como valor de cálculo; k: fator escala.

2.5. Verificação do mecanismo de ruptura a cortante
Como já apresentado anteriormente, existem basicamente dois mecanismos distintos de ruptura por cisalhamento para lajes alveolares: tração diagonal e flexo-cortante. Enquanto o carregamento solicitante não é capaz de provocar fissuras de flexão na laje, o mecanismo de tração diagonal é determinante na resistência a força cortante, ou seja, conhecendo o valor do momento de fissuração (Mr) da laje na seção crítica em análise, e o momento atuante (Ma) na mesma seção, é possível descobrir qual o mecanismo resistente que representa o elemento analisado. Outro aspecto importante é a verificação da seção na situação em vazio, onde as perdas de protensão ainda não são totais e a peça não se encontra carregada. Neste momento podem surgir fissuras de flexão na fibra superior que poderão definir a seção de ruptura por cisalhamento. Este assunto, porém, será abordado em outro trabalho, assumindo aqui atendido este critério. 
Para a situação de laboratório, conforme Figura 5, onde a ordem de grandeza da carga P do atuador é muito superior à carga distribuída de peso próprio, aqui representada pela notação g1, o momento atuante do comprimento da peça até a posição x=a, pode ser expresso por: